Practice Model questions set 1 - quantitative aptitude Online Quiz (set-1) For All Competitive Exams
Q-1) In the figure given below, PQ is parallel to RS and PR is parallel to QS. If ∠LPR = 35° and ∠ UST = 70°, then what is ∠MPQ equal to ?
(a)
(b)
(c)
(d)
![]()
PQ || RS
PR|| QS
∴ PQRS is a || gm
∠LPR = 35° and ∠UST = 70°
∠UST = ∠RSQ (Vertically opposite)
∠RSQ = ∠RPQ (opposite angle of 11 gm)
∠LPR + ∠RPQ + ∠MPQ = 180°
35° + 70° + ∠MPQ = 180°
∠MPQ = 180 – 105
∠MPQ = 75°
Q-2) The diagonals of a trapezium are at right angles, and the slant sides, if produced, form an equilateral triangle with the greater of the two parallel sides. If the area of the trapezium is 16 square cm, then the distance between the parallel sides is
(a)
(b)
(c)
(d)
![]()
ΔEAB is equilateral
ΔEDC is also equilateral
Area of trapezium ABCD
= $(1/2 × DB × OA) + 1/2 (DB × OC)$
= $1/2$ × DB × AC
Let AO = OB = x and DO = OC = y
Area (ABCD) = $1/2 (x + y)^2$ = 16(given)
⇒ x + y = 4 $√2$ ... (i)
ΔAOB is a right angled isosceles triangle.
So, AB = $√{x^2 + x^2} = √2x$
Similarly, DC = $√2$y
Now, FG = EF – EG
⇒ FG = AB sin 60° – DC sin 60°
= $√3/2 (AB - DC) = √6/2$ (x - y) ... (ii)
Area of trapezium
= Area ΔEAB – Area ΔEDC
= $√3/4 (AB^2 - DC^2)$
= $√3/4 [(x√2)^2 - (y√2)^2]$
⇒ Area = $√3/2$ (x + y) (x – y)
Now, $√3/2$ (x + y)(x - y) = 16
⇒ x – y = ${32}/{√3 (x + y)} ⇒ x - y = 8/√6 (∵ x + y = 4√2)$
Height = $√6/2 (x - y) = √6/2 × 8/√6$ = 4 cm
Q-3) 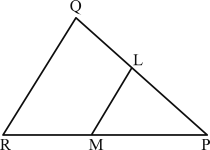
In the figure given above, LM is parallel to QR. If LM divides the ΔPQR such that area of trapezium LMRQ is two times the area of ΔPLM, then what is ${PL}/{PO}$ equal to?
(a)
(b)
(c)
(d)
In the given figure.
ar MRQL = 2 ar ΔPLM
Let area of ΔPLM be x, then
∴ the area of trapezium = 2x
∴ ar ΔPQR = 2x + x = 3x
Here it is clear from the given figure that ΔPQR ∼ ΔPLM
![]()
∴ ${\text"ar ΔPQR"}/{\text"ar ΔPLM"} = {3x}/x$
${PL^2}/{PQ^2} = 1/3 ∴ = {PL}/{PQ} = 1/√3$
Q-4) The dimensions of a field are 15 m by 12 m. A pit 8 m long, 2.5 m wide and 2 m deep is dug in one corner of the field and the earth removed is evenly spread over the remaining area of the field. The level of the field is raised by
(a)
(b)
(c)
(d)
![]()
Volume of pit = l b h = 8 × 2.5 × 2 = 40 $m^3$.
Let the label of the earth spread over remaining area = h.
Volume of the earth spread = Volume of a pit
⇒ [(12 × 15) – (8 × 2.5)] × h = 40
∴ h = ${40}/{180 - 20} = {40}/{160} = 1/4$m = 25 cm
Q-5) A right circular cylinder just encloses a sphere. If p is the surface area of the sphere and q is the curved surface area of the cylinder, then which one of the following is correct?
(a)
(b)
(c)
(d)
p = 4π$r^2$
q = 2πr.h = 2πr. 2r
= 4π $r^2$
Hence, P = q.
![]()
Q-6) The perimeter of a triangular field is 240 m. If two of its sides are 78 m and 50 m, then what is the length of the perpendicular on the side of length 50 m from the opposite vertex?
(a)
(b)
(c)
(d)
Given, 2s = 240 ⇒ s = 120 and c = 50m, b = 78 m, a = 112m
∴ Area of triangle = $1/2$ × Base × Height
![]()
and also, Δ = $√{s(s - a)(s - b)(s - c)}$
∴ = $√{120(120 - 112)(120 - 78)(120 - 50)}$
= $√{120 × 8 × 42 × 70} = 1680 m^2$
∵ Area of triangle
= $1/2$ × Base × Height
⇒ 1680 = $1/2$ × 50 × h
∴ h = ${2 × 1680}/{50}$ = 67.2m
Q-7) Consider an equilateral triangle of a side of unit length. A new equilateral triangle is formed by joining the midpoints of one, then a third equilateral triangle is formed by joining the mid-points of second. The process is continued. The perimeter of all triangles, thus formed is
(a)
(b)
(c)
(d)
Sides of equilateral triangle are follows:
3, $3/2, 3/4, 3/8$ ... so on
These sequence formed a GP serves.
So sum of GP for Infinite terms.
S = $a/{1 - r}$
Here a = 3, r = $1/2$
S = $3/{1 - 1/2}$ =6 units
Q-8) Two straight lines AB and AC include an angle. A circle is drawn in this angle which touches both these lines. One more circle is drawn which touches both these lines as well as the previous circle. If the area of the bigger circle is 9 times the area of the smaller circle, then what must be the angle A?
(a)
(b)
(c)
(d)
![]()
Let the radius of the bigger circle be a and radius of the smaller circle be b.
Then the angle made by direct common tangents when two circles of radius a and b touch externally is given by θ = $2sin^{- 1}({a - b}/{a + b})$
We are given that area of the bigger circle = 9 area of the smaller circle
⇒ $πa^2 = 9πb^2 ⇒ a^2 = 9b^2 ⇒ a = 3b$
Let us consider ∠BAC = θ
Thus,
θ = $2 sin^{-1} ({a - b}/{a + b}) = 2 sin^{-1} ({3b - b}/{3b + b}) = 2sin^{-1} ({2b}/{4b})$
= $2 sin^{-1} (1/2) = 2 sin^{-1}$ (sin 30°) = 2 × 30° = 60°
Q-9) In the figure given above, ABCD is a trapezium. EF is parallel to AD and BG. ∠y is equal to
(a)
(b)
(c)
(d)
From figure.
![]()
BC || EF || AD
∴ x° = z° = 50° (corresponding interior angle
∴ θ + z° = 180° (linear pair)
∴ ∼ θ = 180° – 50° = 130°
In quadrilateral
AQFD, x° + y° + 120° + θ = 360°
50° + y° + 120° + 130° = 360°
y = 360° – 300° = 60°
Q-10) PQ is a common chord of two circles. APB is a secant line joining points A and B on the two circles. Two tangents AC and BC are drawn. If ∠ACB = 45°, then what is ∠AQB equal to?
(a)
(b)
(c)
(d)
The tangents drawn from an outer point on a circle are always equal = ∠CBA.
Therefore, ∠CAB = ∠CBA
![]()
∴ 45° + x + x = 180°
⇒ 2x = 180° – 45°
⇒ x = 67 ${1°}/2$
∠AQP = ∠x = ∠BQP
= 67 ${1°}/2$
(alternate interior segments properties)
⇒ ∠AQB = ∠AQP + ∠BQP
= $67 {1°}/2 + 67{1°}/2$ = 135°